Fractal-Fractional Order Ordinary Differential Equations
The concept of fractal–fractional differentiation has appeared as a combination of two mathematical concepts: fractal differentiation and fractional differentiation. These operators are helpful for modeling more complex problems, also they allow us to understand many physical problems which have fractal properties.
Fractal-fractional derivative with power law:
\[{^{FFP}_aD^{\gamma,\theta}_t}u(t)=\frac{1}{\Gamma(1-\gamma)}\frac{d}{dt^\theta}\int_a^tu(y)(t-y)^{-\gamma}dy,\ 0<\gamma, \theta\leq1\]
Fractal-fractional derivative with exponential decay kernel:
\[{^{FFE}_aD^{\gamma,\theta}_t}u(t)=\frac{M(\gamma)}{\Gamma(1-\gamma)}\frac{d}{dt^\theta}\int_a^tu(y)\exp(\frac{-\gamma}{1-\gamma}(t-y))dy,\ 0<\gamma, \theta\leq1\]
Fractal-fractional derivative with Mittag Leffler kernel:
\[{^{FFM}_aD^{\gamma,\theta}_t}u(t)=\frac{AB(\gamma)}{\Gamma(1-\gamma)}\frac{d}{dt^\theta}\int_a^tu(y)E_\gamma(\frac{-\gamma}{1-\gamma}(t-y))dy,\ 0<\gamma, \theta\leq1\]
Fractal-fractional ODE system
To construct fractal-fractional differential problems, we need to use FFPODEProblem, FFEODEProblem and FFMODEProblem to define our problem:
julia> FFPODEProblem(f, [α, β], u0, tspan)
julia> FFEODEProblem(f, [α, β], u0, tspan)
julia> FFMODEProblem(f, [α, β], u0, tspan)Let's see the Lorenz system in Atangana-Baleanu-Caputo sense with Mittag Leffler kernel:
\[\begin{cases} {^{FFM}D^{\alpha,\beta}}x=a(y-x)\\ {^{FFM}D^{\alpha,\beta}}y=(b-z)x-y\\ {^{FFM}D^{\alpha,\beta}}z=xy-cz \end{cases}\]
using FractionalDiffEq, Plots
α=1;β=1;h=0.01;tspan=(0, 50)
u0 = [-2, 1, -1]
function fun(du, u, p, t)
a=10;b=28;c=8/3
du[1] = a*(u[2]-u[1])
du[2] = (b-u[3])*u[1]-u[2]
du[3] = u[1]*u[2]-c*u[3]
end
prob = FFODEProblem(fun, [α, β], u0, tspan)
sol = solve(prob, h, AtanganaSeda())
plot3d(sol, vars=(1,2,3) title="Fractal-fractional Order Lorenz System")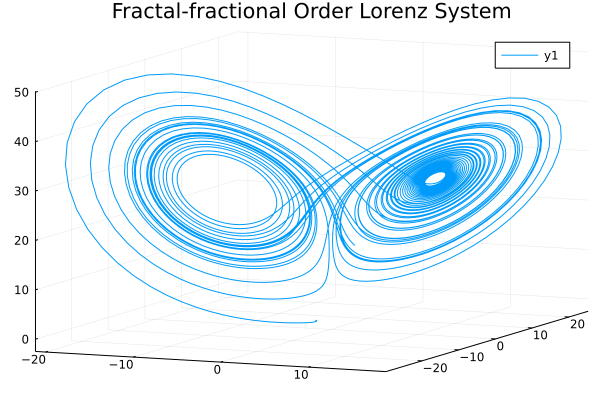
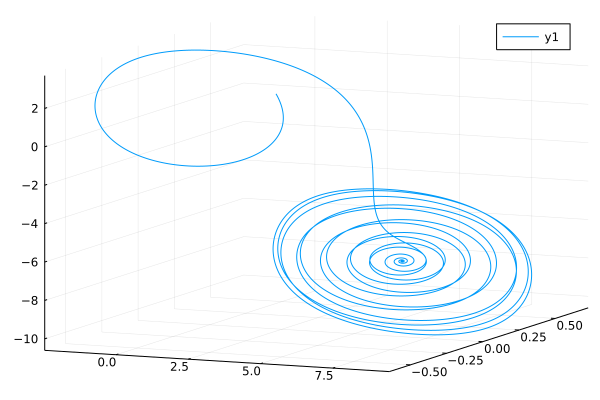
Variable order fractal-fractional ODE problem
using FractionalDiffEq, Plots
alpha=0.96;h=0.01;tfinal=100;
β(t) = 0.01+0.01*t
u0=[-0.2; 0.5; 0.2]
function fun(du, u, p, t)
gama=10.814;lambda=14;a=0.2;b=0.15;
du[1] = gama*(u[2]-a*sin(2*pi*b*u[1]))
du[2] = u[1]-u[2]+u[3]
du[3] = -lambda*u[2]
end
prob = FFODEProblem(fun, [alpha, β], u0, (1, tfinal))
sol = solve(prob, h, AtanganaSeda())
plot3d(sol, vars=(1,2,3))