Multi-term FODE
By specifying different orders in the equation, we can handle multi-terms FODE now!
Let's see if we have an initial value problem with multiple terms derivative containing both fractional and integer, we can use the PIEX algorithm to solve the equation.
All we need to do is passing the parameters and orders of the fractional ordinary differential equation to the API solve as two arrays.
When we are solving the multi-terms FODE problem, please note we should keep the parameters array and orders array have the same length.
Detailed Usage
We need to first define our multi-terms FODE problem:
julia> prob = MultiTermsFODEProblem(parameters, orders, rightfun, u0, tspan)Let's see if we have an equation like:
\[2y''(t)+4D^{1.5}y(t)=1\]
To solve the multi-terms fractional order equation, you can use the code:
rightside = 1
prob = MultiTermsFODEProblem([2, 4], [2, 1.5], rightside, [0, 0], (0, 30))
sol = solve(prob, PIEX(), dt=0.01)Bingo! The result sol is the numerical solution of this equation!!!!
Example
We have an initial problem:
\[y'''(t)+\frac{1}{16} {^C_0D^{2.5}_ty(t)}+\frac{4}{5}y''(t)+\frac{3}{2}y'(t)+\frac{1}{25}{^C_0D^{0.5}_ty(t)}+\frac{6}{5}y(t)=\frac{172}{125}\cos(\frac{4t}{5})\]
\[y(0)=0,\ y'(0)=0,\ y''(0)=0\]
Model this problem and solve the equation:
using FractionalDiffEq, Plots
tspan = (0, 30)
rightfun(x, y) = 172/125*cos(4/5*x)
prob = MultiTermsFODEProblem([1, 1/16, 4/5, 3/2, 1/25, 6/5], [3, 2.5, 2, 1, 0.5, 0], rightfun, [0, 0, 0, 0, 0, 0], tspan)
sol = solve(prob, PIEX(), dt=0.01)
plot(sol, legend=:bottomright)By solving the equation and plotting the result, we can see its solution here:
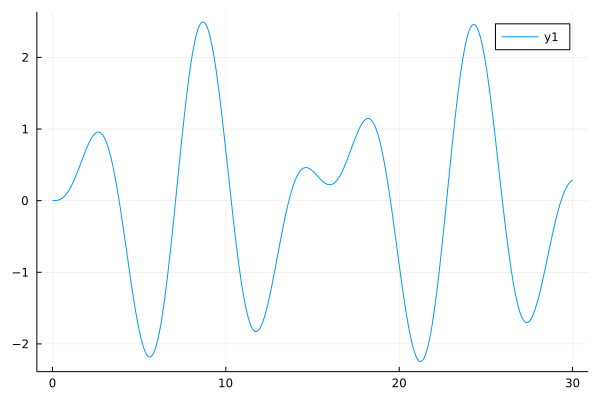
This example is an official example in the source code, please see the example folder