Mittag Leffler function

For more intreresting topics and applications about Mittag Leffler function, we recommend you to read Mittag-Leffler Functions, Related Topics and Applications

Being called "The Queen Function of the Fractional Calculus", Mittag Leffler function plays an important role in fractional order computing and modeling. Here, we classify the Mittag Leffler function into three types:

Classical Mittag Leffler function(Single-Parametric version)

The Mittag Leffler function is defined by Gösta Magnus Mittag-Leffler by a power series as:

\[E_\alpha(z)=\sum_{k=0}^{\infty}\frac{z^k}{\Gamma(\alpha k+1)},\ (\alpha\in\mathbb{C})\]

Two-Parametric Mittag Leffler function

The two-parametric Mittag Leffler function as the generalization of the classical Mittag Leffler function :

\[E_{\alpha,\ \beta}(z)=\sum_{k=0}^{\infty}\frac{z^k}{\Gamma(\alpha k+\beta)},\ (\mathfrak{Re}(\alpha)>0,\ \beta\in\mathbb{C})\]

Three-Parametric Mittag Leffler function

FractionalDiffEq.jl also supports the three-parametric Mittag Leffler function(The Prabhakar function):

\[E_{\alpha,\ \beta}^\gamma(z)=\sum_{k=0}^{\infty}\frac{(\gamma)_k z^k}{k!\Gamma(\alpha k+\beta)},\ (\mathfrak{Re}(\alpha)>0,\ \mathfrak{Re}(\beta)>0,\ \gamma\in\mathbb{C})\]

Here $(\gamma)_k=\frac{\Gamma(\gamma+k)}{\Gamma(\gamma)}$ is the Pochhammer symbol.

In FractionalDiffEq.jl, you can compute the three types of Mittag Leffler functions by calling:

julia> mittleff(α, z)
julia> mittleff(α, β, z)
julia> mittleff(α, β, γ, z)

Also, you can compute the derivative of the Mittag Leffler function by calling:

julia> mittleffderiv(α, β, z)

To compute Mittag Leffler function error:

julia> mittlefferr(α, z, ρ)
julia> mittlefferr(α, β, z, ρ)

Here, ρ is the targeting accuracy.

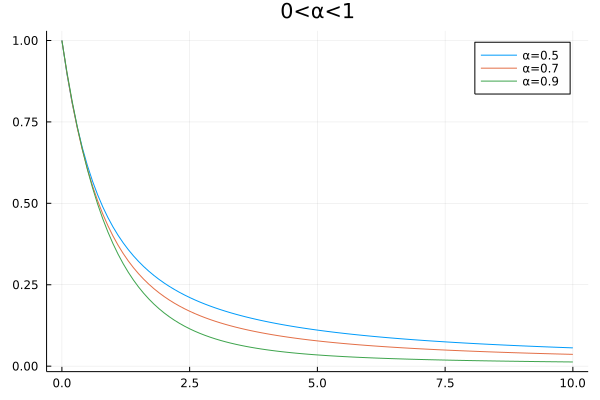
Different order classical Mittag Leffler function plot($0<\alpha<1$):

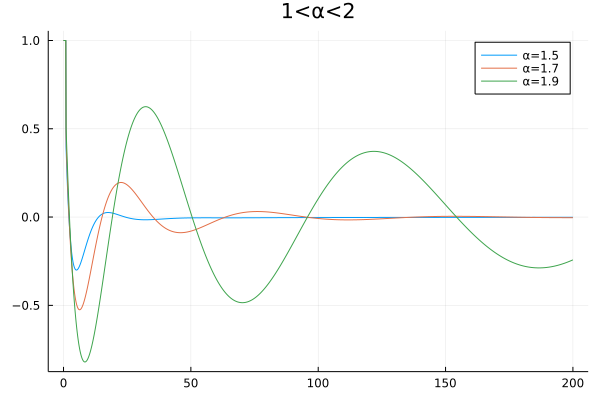
And also $1<\alpha<2$:

If we input complex number to Mittag Leffler function, for example:

\[E_{0.8, 0.9}(z)\]